Ever since I owned my first Amiga, I've always been interested in how it seemed to be able to do so many things at the same time. Not just running multiple programs at the same time, but also running the Blitter and the CPU at the same time. It almost seemed to be magic back in the 1980's and 1990's. So when I started learning how to properly code for the Commodore Amiga's hardware around 2015, I obviously looked up just how the Blitter and CPU could run at the same time.
As it turns out, the Blitter and CPU accomplish this by having one of them (the Blitter) occasionally giving the other (the CPU) some time to do its thing. Which in many ways was a dissapointing answer, but also led me to experiment quite a bit with optimising how this split could be best used. Now my main platform of choice at the time was the A500. Which meant that most of these experiments led to a failure to increase performance in any meaningful way.
Then, during summer 2019, I had an idea… What about the A1200?
Its AGA chipset allows the CPU to access Chip memory 32 bits at a time. And the 68020 that powers it is much faster than the 68000 found in the A500. That might just change things. I ended up posting some thoughts and questions about this on the English Amiga Board. After some discussion over there, I came to a conclusion: it may be possible to use the Blitter and CPU together in a way that actually helps performance.
CPU Assisted Blitting for the A1200
As it turns out, the Blitter and CPU accomplish this by having one of them (the Blitter) occasionally giving the other (the CPU) some time to do its thing. Which in many ways was a dissapointing answer, but also led me to experiment quite a bit with optimising how this split could be best used. Now my main platform of choice at the time was the A500. Which meant that most of these experiments led to a failure to increase performance in any meaningful way.
Then, during summer 2019, I had an idea… What about the A1200?
Its AGA chipset allows the CPU to access Chip memory 32 bits at a time. And the 68020 that powers it is much faster than the 68000 found in the A500. That might just change things. I ended up posting some thoughts and questions about this on the English Amiga Board. After some discussion over there, I came to a conclusion: it may be possible to use the Blitter and CPU together in a way that actually helps performance.
CPU Assisted Blitting for the A1200
Above: testing the CPU Assisted Blitting program in WinUAE.
To make a long story considerably shorter: after quite some experimentation, it does indeed turn out you can have the A1200's CPU assist the Blitter and gain extra blitting performance by doing so. Not only that, but this actually holds for both operations commonly used for blitting bobs. Both copy and cookie-cut operations can be made to run faster when combining the CPU and Blitter, rather than just running one or the other.
In a move that probably shouldn't surprise anyone by now, I've decided to make an example program that shows this in action. As you might have expected, I've also made a video of the program in action and this article (which explains how it all works). Naturally, the full source code is also available for download :)
The basic idea is to run the Blitter without BLTPRI set, so the CPU gets at least one in four cycles to Chip memory. Then, make the CPU do part of the same blit as the Blitter. Because the CPU reads or writes 32 bits at a time whenever it accesses Chip memory*, it is twice as efficient as the Blitter during those cycles. Normally, this extra efficiency is canceled out by the slow access times of the CPU to Chip memory. But when the Blitter is running, all the cycles that the CPU can't access Chip memory go to the Blitter instead.
You can couple this with choosing specific Blitter channel combinations that force extra idle cycles**, to get a boost in performance. Sadly however, it's not all good news. The performance gain is modest in all cases and only copy blits can add extra idle cycles in a useful way. But, the results are still positive overall - even for cookie-cut blits.
It's worth noting that this method will work on all Amiga's with 32 bit Chip memory (A1200, CD32, A3000 and A4000).
*) Assuming data in Chip memory is aligned on 32 bit boundaries, which the example program enforces.
**) Idle cycles aren't used by the Blitter (or other DMA sources) but can be used by the CPU.
In a move that probably shouldn't surprise anyone by now, I've decided to make an example program that shows this in action. As you might have expected, I've also made a video of the program in action and this article (which explains how it all works). Naturally, the full source code is also available for download :)
The basic idea is to run the Blitter without BLTPRI set, so the CPU gets at least one in four cycles to Chip memory. Then, make the CPU do part of the same blit as the Blitter. Because the CPU reads or writes 32 bits at a time whenever it accesses Chip memory*, it is twice as efficient as the Blitter during those cycles. Normally, this extra efficiency is canceled out by the slow access times of the CPU to Chip memory. But when the Blitter is running, all the cycles that the CPU can't access Chip memory go to the Blitter instead.
You can couple this with choosing specific Blitter channel combinations that force extra idle cycles**, to get a boost in performance. Sadly however, it's not all good news. The performance gain is modest in all cases and only copy blits can add extra idle cycles in a useful way. But, the results are still positive overall - even for cookie-cut blits.
It's worth noting that this method will work on all Amiga's with 32 bit Chip memory (A1200, CD32, A3000 and A4000).
*) Assuming data in Chip memory is aligned on 32 bit boundaries, which the example program enforces.
**) Idle cycles aren't used by the Blitter (or other DMA sources) but can be used by the CPU.
- Method
- Copy algorithm
- Cookie-cut algorithm
- Performance
- Notes & caveats
Tab 1
In a nutshell, the biggest problem to solve is keeping both the CPU and the Blitter busy doing useful work. My solution is to have the Blitter blit the top lines of any blit* and have the CPU blit the bottom lines of the same blit. How many lines the Blitter draws and how many lines the CPU draws is determined ahead of time by a routine that measures the performance of all possible mixes of line numbers. This routine is only required to determine the optimum mix once. So it's also possible to do these tests completely separately from the program itself and simply store the results in a table that is included in the main program.
*) The example provides copy & cookiecut blitting routines for the CPU and routines for combined CPU/Blitter copy & cookiecut blitting.
This method has the advantage of being simple to implement compared to alternatives and is very effective at splitting CPU and Blitter resources for the purposes of blitting.
As pointed out earlier in this article, the reason running the Blitter and CPU at the same time improves performance has everything to do with the AGA Chip memory bus. By running the Blitter and CPU at the same time, bus utilisation is enhanced. An example of how this works is shown in the following image.
*) The example provides copy & cookiecut blitting routines for the CPU and routines for combined CPU/Blitter copy & cookiecut blitting.
This method has the advantage of being simple to implement compared to alternatives and is very effective at splitting CPU and Blitter resources for the purposes of blitting.
As pointed out earlier in this article, the reason running the Blitter and CPU at the same time improves performance has everything to do with the AGA Chip memory bus. By running the Blitter and CPU at the same time, bus utilisation is enhanced. An example of how this works is shown in the following image.
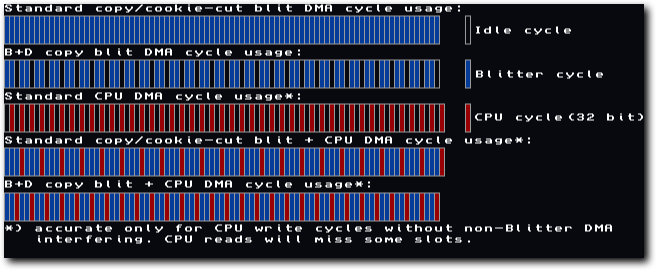
Above: a diagram showing theoretical Blitter and CPU DMA cycle usage
Note that the diagrams above show an idealised version of what is actually going on. In reality the mix of CPU/Blitter cycles allocated will almost certainly be somewhat different. Thus the improvements in performance will be somewhat muted, compared to what you might expect when looking at these diagrams.
A final point about CPU/Blitter concurrency
It should be noted here that it's also possible to use the CPU for non-blitting tasks, while the Blitter is running, to increase overall system performance. However, this is often difficult to do effectively - especially as the total amount of pixels that are being blit starts to rise. Blitting large amounts of pixels often leads to times during which the CPU will be effectively idle, even with clever coding.
Also note that achieving the best possible performance might require dynamically switching (some) interrupts off prior to each blit and back on again after each blit. This is to prevent the CPU doing other work (such as playing a module) during the blits themselves. It's also possible the effect of allowing such interrupts is minimal though - I have not tested this.
In any case, the main bottleneck for Amiga games is quite often a simple lack of "Blitter oomph", rather than a shortage of CPU power. The method outlined in this article alleviates this problem by increasing the amount of pixels that can be blit per frame.
A final point about CPU/Blitter concurrency
It should be noted here that it's also possible to use the CPU for non-blitting tasks, while the Blitter is running, to increase overall system performance. However, this is often difficult to do effectively - especially as the total amount of pixels that are being blit starts to rise. Blitting large amounts of pixels often leads to times during which the CPU will be effectively idle, even with clever coding.
Also note that achieving the best possible performance might require dynamically switching (some) interrupts off prior to each blit and back on again after each blit. This is to prevent the CPU doing other work (such as playing a module) during the blits themselves. It's also possible the effect of allowing such interrupts is minimal though - I have not tested this.
In any case, the main bottleneck for Amiga games is quite often a simple lack of "Blitter oomph", rather than a shortage of CPU power. The method outlined in this article alleviates this problem by increasing the amount of pixels that can be blit per frame.
Tab 2
The combined copy blit algorithm combines a basic CPU memory copy (with support for rectangular blits) and a standard copy blit running on the Blitter. The Blitter copy uses channels B & D, rather than the standard channel combination (A & D). This is done to increase the number of cycles the CPU gets to access memory (up from one in four to one in three). The Blitter blits the topmost lines, while the CPU blits the bottommost lines.
The CPU based copy routine as implemented forces longword alignment for optimal speed and supports blits of any height.
A B&D blit has one idle cycle after every two Blitter cycles rather than the usual one CPU cycle after every three Blitter cycles you get with a A&D blit. Choosing this type of blit helps increase performance. The end result is that a combined copy blit runs faster than just using the Blitter.
The CPU based copy routine as implemented forces longword alignment for optimal speed and supports blits of any height.
A B&D blit has one idle cycle after every two Blitter cycles rather than the usual one CPU cycle after every three Blitter cycles you get with a A&D blit. Choosing this type of blit helps increase performance. The end result is that a combined copy blit runs faster than just using the Blitter.
Implementation details
After some testing, I created two routines for copy blits. Both are aimed at restoring bobs and are not well suited for general bitmap copying. One of the routines is a generic routine that supports copies of up to 20 longwords in width. The other is an optimised two-longword wide copy. Note that the workload is split in a smart way for both routines: the Blitter will only copy three words for a 32 pixel wide object+shift, the CPU will copy two longwords for the same.
The main optimisation employed by the optimised version is to unroll the copy loop once (copying two bitplanes per loop instead of one). It also removes the choice of different widths.
Note: it's highly likely that unrolling the loop in the generic version in the same way will cause very similar improvements in performance. The cost is only allowing blits with either an even number of lines or an even number of bitplanes. I left the generic code as is to serve as an example to build on. Please note: the generic copy routine as presented is only faster than using the Blitter in case of larger blits (>32x32 pixels). The optimised version is faster for bigger and smaller blits (32x32).
Both routines consist of a sequence of move.l (ax)+,(ax)+ and add.l dx,ax instructions. For (very) wide copy blits, movem.l is used instead for reading/writing.
After some testing, I created two routines for copy blits. Both are aimed at restoring bobs and are not well suited for general bitmap copying. One of the routines is a generic routine that supports copies of up to 20 longwords in width. The other is an optimised two-longword wide copy. Note that the workload is split in a smart way for both routines: the Blitter will only copy three words for a 32 pixel wide object+shift, the CPU will copy two longwords for the same.
The main optimisation employed by the optimised version is to unroll the copy loop once (copying two bitplanes per loop instead of one). It also removes the choice of different widths.
Note: it's highly likely that unrolling the loop in the generic version in the same way will cause very similar improvements in performance. The cost is only allowing blits with either an even number of lines or an even number of bitplanes. I left the generic code as is to serve as an example to build on. Please note: the generic copy routine as presented is only faster than using the Blitter in case of larger blits (>32x32 pixels). The optimised version is faster for bigger and smaller blits (32x32).
Both routines consist of a sequence of move.l (ax)+,(ax)+ and add.l dx,ax instructions. For (very) wide copy blits, movem.l is used instead for reading/writing.
Tab 3
The combined cookie-cut blit algorithm combines a CPU based cookie-cut algorithm and a standard cookie-cut blit running on the Blitter. Unlike the copy algorithm, no special channel combination exists to increase the number of idle cycles. As such, the CPU gets access to no more than one in four DMA cycles. As with the copy algorithm, the Blitter blits the topmost lines, the CPU blits the bottommost lines.
The CPU based cookie-cut routine as implemented forces longword alignment for optimal speed and supports blits of any height.
The main problem with a cookie-cut algorithm running on the CPU is that you need to perform a number operations that end up being fairly expensive when combined. Normally this causes the CPU to be too slow to be useful for blitting. However, this changes when running this kind of algorithm while the Blitter is also running. In that case many of these operations are "hidden" by Blitter activity while the CPU works from the cache. Keep in mind however that memory accesses can't be hidden.
All in all, the CPU needs to do three read operations and one write operation per longword blit. It also needs to shift or rotate both the mask and bob data in place and combine the mask, bob data and destination. There are many different ways to write such a routine and I experimented with a whole bunch of different variations. I tried routines based on logical shifts, rotates and bitfield instructions. I also tried a variety of instruction orders to try and get optimal timing. I even tried routines that used various levels of pre-shifting.
In my testing, using bitfield instructions or pre-shifting was either a) always slower (pre-shifting) or b) slower in most scenarios (bitfields), when compared to rotating/shifting. Of the two remaining options, shifting is ever so slightly faster* and thus is what I went with.
*) This was surprising, as the rotate based example actually uses fewer instructions and amounts to fewer cycles according to the MC68020 manual. This once again shows it's important to always test assumptions "in the real world". Do note the actual difference between these two approaches was pretty small.
The CPU based cookie-cut routine as implemented forces longword alignment for optimal speed and supports blits of any height.
The main problem with a cookie-cut algorithm running on the CPU is that you need to perform a number operations that end up being fairly expensive when combined. Normally this causes the CPU to be too slow to be useful for blitting. However, this changes when running this kind of algorithm while the Blitter is also running. In that case many of these operations are "hidden" by Blitter activity while the CPU works from the cache. Keep in mind however that memory accesses can't be hidden.
All in all, the CPU needs to do three read operations and one write operation per longword blit. It also needs to shift or rotate both the mask and bob data in place and combine the mask, bob data and destination. There are many different ways to write such a routine and I experimented with a whole bunch of different variations. I tried routines based on logical shifts, rotates and bitfield instructions. I also tried a variety of instruction orders to try and get optimal timing. I even tried routines that used various levels of pre-shifting.
In my testing, using bitfield instructions or pre-shifting was either a) always slower (pre-shifting) or b) slower in most scenarios (bitfields), when compared to rotating/shifting. Of the two remaining options, shifting is ever so slightly faster* and thus is what I went with.
*) This was surprising, as the rotate based example actually uses fewer instructions and amounts to fewer cycles according to the MC68020 manual. This once again shows it's important to always test assumptions "in the real world". Do note the actual difference between these two approaches was pretty small.
Implementation details
I ended up up with two routines for cookie-cut blits.
One optimised routine for blitting objects that are up to 32 pixels wide* (most optimal for objects >16 pixels wide) and one generic routine. The generic routine is slower, but still offers an increase in performance over using just the Blitter (even for 32 pixel wide objects). It also supports objects of any width. The example program only shows the optimised routine in action, but still contains the full code of the generic routine for reference. The generic routine can probably be optimised further, I left it as is to have an example of how to approach writing such a routine.
Note that, just like the copy blits, the workload is split in a smart way: the Blitter will only blit three words for a 32 pixel wide object+shift, the CPU will blit two longwords for the same. Also note, to cookie-cut using the CPU+Blitter, the image and mask data stored must be a multiple of 32 bits in width. For optimal performance, the data must also be aligned in memory to multiples of 32 bits. These limits are valid for both the generic and optimised routines.
*) This excludes the required space for shifting, so it is actually a two longword wide blit.
The generic cookie-cut routine works as follows:
1. read one longword of the mask
2. shift/rotate it by the correct amount, keep the remainder ready for the next longword
3. read one longword of the source
4. shift/rotate it by the correct amount, keep the remainder ready for the next longword
5. read one longword of the destination
6. mask out the mask (not/and)
7. combine with source (or)
8. write longword of destination back
9. repeat this until reaching the width of the object
10. read one more longword, combine it with the remainder as in points 6&7 and write it back.
11. move to the next line until out of lines
The optimised cookie-cut routine changes this as follows:
1. read one longword of the mask
2. shift/rotate it by the correct amount, keep the remainder
3. use the now calculated mask for all planes of this line without reading/calculating it again
4. now follow the same steps as in the generic routine, but skip the width loop (steps 3-11, but not step 9)
The difference between the two is that the optimised routine uses two registers to keep the full mask for each line in registers for all planes, rather than reading a new mask value for every plane. This can't be done for objects of arbitrary width without having an arbitrary number of registers. Hence, it's currently limited to blits of a single longword (plus shifting space).
I'm pretty sure the optimised routine can be rewritten so that you have at least one extra free register, which would allow it to do two-longword wide blits as well. It's also possible that better approaches might exist for optimising cookie-cut blits, without further limiting what can be blit. I am not personally aware of them at this time, but I'm always open to new ideas. If you know of a better approach or have other ideas on how to make this work better still, drop me a line :)
I ended up up with two routines for cookie-cut blits.
One optimised routine for blitting objects that are up to 32 pixels wide* (most optimal for objects >16 pixels wide) and one generic routine. The generic routine is slower, but still offers an increase in performance over using just the Blitter (even for 32 pixel wide objects). It also supports objects of any width. The example program only shows the optimised routine in action, but still contains the full code of the generic routine for reference. The generic routine can probably be optimised further, I left it as is to have an example of how to approach writing such a routine.
Note that, just like the copy blits, the workload is split in a smart way: the Blitter will only blit three words for a 32 pixel wide object+shift, the CPU will blit two longwords for the same. Also note, to cookie-cut using the CPU+Blitter, the image and mask data stored must be a multiple of 32 bits in width. For optimal performance, the data must also be aligned in memory to multiples of 32 bits. These limits are valid for both the generic and optimised routines.
*) This excludes the required space for shifting, so it is actually a two longword wide blit.
The generic cookie-cut routine works as follows:
1. read one longword of the mask
2. shift/rotate it by the correct amount, keep the remainder ready for the next longword
3. read one longword of the source
4. shift/rotate it by the correct amount, keep the remainder ready for the next longword
5. read one longword of the destination
6. mask out the mask (not/and)
7. combine with source (or)
8. write longword of destination back
9. repeat this until reaching the width of the object
10. read one more longword, combine it with the remainder as in points 6&7 and write it back.
11. move to the next line until out of lines
The optimised cookie-cut routine changes this as follows:
1. read one longword of the mask
2. shift/rotate it by the correct amount, keep the remainder
3. use the now calculated mask for all planes of this line without reading/calculating it again
4. now follow the same steps as in the generic routine, but skip the width loop (steps 3-11, but not step 9)
The difference between the two is that the optimised routine uses two registers to keep the full mask for each line in registers for all planes, rather than reading a new mask value for every plane. This can't be done for objects of arbitrary width without having an arbitrary number of registers. Hence, it's currently limited to blits of a single longword (plus shifting space).
I'm pretty sure the optimised routine can be rewritten so that you have at least one extra free register, which would allow it to do two-longword wide blits as well. It's also possible that better approaches might exist for optimising cookie-cut blits, without further limiting what can be blit. I am not personally aware of them at this time, but I'm always open to new ideas. If you know of a better approach or have other ideas on how to make this work better still, drop me a line :)
Tab 4
The performance gained by this way of blitting is modest, but still overall worthwhile in my opinion. Interestingly, the optimised cookie-cut blit actually adds relatively more performance than the copy blit. This was not what I expected, as the copy blit merely copies memory, while the cookie-cut blit does several other operations as well.
That said, combining the two routines still offers a noticeable speedup for blitting bobs. So considering this way of doing things is clearly worthwhile - especially if you keep in mind that this effect doesn't really change the amount of memory needed*. Unless your code is already interleaving the Blitter and CPU very effectively, using this method will almost certainly provide a useful speed boost.
*) for objects that are multiples of 32 bits wide, the maximum extra memory cost is at most one extra word per bob & mask. Objects that are not multiples of 32 bits wide will further cost an extra word per plane per line of both mask and image data.
One thing of note is the effect of other DMA channels on the bus (bitplane DMA, Copper, etc). In general, increasing DMA load will increase the relative performance gain compared to only using the Blitter. This remains true as long as there are at least some cycles available for CPU/Blitter.
For reference, I've included two tables. The first table shows both the number of 32x32 bobs that can be blit per PAL frame, as well as a percentage improvement (or loss) compared to running the same on the Blitter. The given percentage is based on measurements using the CIA timers**, which is far more accurate than a simple bob count. The second table shows numbers for 64x64 bobs instead, showing that relative performance gains increase as bob size increases - achieving decent results even when using the non-optimal generic routines.
In all cases the screen size used was 288x244x6, plus a small 288x16x3 status bar. Percentages and other results will vary with different screen sizes and depths. Note that the generic routines are meant more as an example showing how to approach this problem, not as fully optimised routines. As such, they will give poorer results when compared to the optimised routines in the same situation.
That said, combining the two routines still offers a noticeable speedup for blitting bobs. So considering this way of doing things is clearly worthwhile - especially if you keep in mind that this effect doesn't really change the amount of memory needed*. Unless your code is already interleaving the Blitter and CPU very effectively, using this method will almost certainly provide a useful speed boost.
*) for objects that are multiples of 32 bits wide, the maximum extra memory cost is at most one extra word per bob & mask. Objects that are not multiples of 32 bits wide will further cost an extra word per plane per line of both mask and image data.
One thing of note is the effect of other DMA channels on the bus (bitplane DMA, Copper, etc). In general, increasing DMA load will increase the relative performance gain compared to only using the Blitter. This remains true as long as there are at least some cycles available for CPU/Blitter.
For reference, I've included two tables. The first table shows both the number of 32x32 bobs that can be blit per PAL frame, as well as a percentage improvement (or loss) compared to running the same on the Blitter. The given percentage is based on measurements using the CIA timers**, which is far more accurate than a simple bob count. The second table shows numbers for 64x64 bobs instead, showing that relative performance gains increase as bob size increases - achieving decent results even when using the non-optimal generic routines.
In all cases the screen size used was 288x244x6, plus a small 288x16x3 status bar. Percentages and other results will vary with different screen sizes and depths. Note that the generic routines are meant more as an example showing how to approach this problem, not as fully optimised routines. As such, they will give poorer results when compared to the optimised routines in the same situation.
Table 1: 32x32 bobs
show
show
show
show
show
show
show
Method
Bobs per PAL frame
% difference (vs A1200/Blitter)
A500 Blitter**
11
64,7%
A1200 Blitter
17
100%
A1200 CPU
8
49,7%
A1200 CPU+Blitter (optimised)
19
113,6%
A1200 CPU+Blitter (generic)
18
106,5%
A1200 CPU+Blitter (generic cookie-cut/optimised copy)
18
109,7%
Table 2: 64x64 bobs
show
show
show
show
Method
Bobs per PAL frame
% difference (vs A1200/Blitter)
A500 Blitter**
3
75%
A1200 Blitter
4
100%
A1200 CPU+Blitter (generic)
5
114,7%
**) A500 numbers were calculated using the method described here and assume 90% efficiency / 10% overhead for setting up the Blitter.
A final point is that the theoretical result differs a bit from the actual result. Looking at the DMA cycle diagram and assuming the CPU should be able to hit every DMA cycle the Blitter gives it, it's possible to calculate an expected result. This result is somewhat higher than the real world results.
My hypothesis is that the main difference is caused by the CPU usually ending up blitting more bytes per line than the Blitter does. This is because of the 32 bit width of the CPU blits vs the 16 bit width used by the Blitter. Other than that, it's possible the CPU doesn't hit all available DMA slots all the time, or that the overhead of the combined blitting routines is big enough to change the result.
For reference, the expected result when just looking at the number of DMA slots the CPU should get would've been around 125% for the generic routines (assuming no other DMA on the bus and blits of equal width).
A final point is that the theoretical result differs a bit from the actual result. Looking at the DMA cycle diagram and assuming the CPU should be able to hit every DMA cycle the Blitter gives it, it's possible to calculate an expected result. This result is somewhat higher than the real world results.
My hypothesis is that the main difference is caused by the CPU usually ending up blitting more bytes per line than the Blitter does. This is because of the 32 bit width of the CPU blits vs the 16 bit width used by the Blitter. Other than that, it's possible the CPU doesn't hit all available DMA slots all the time, or that the overhead of the combined blitting routines is big enough to change the result.
For reference, the expected result when just looking at the number of DMA slots the CPU should get would've been around 125% for the generic routines (assuming no other DMA on the bus and blits of equal width).
Tab 5
The routines I've provided come with some caveats, as does using this method of blitting in general. Also, there's some stuff that is useful to be aware of that didn't really fit in any other section of this article. As such, here's a small list of notes and caveats regarding this method of blitting.
- I found that for this particular purpose, the Amiga Emulators available today overestimate the performance of the 68020 in the A1200. Keep this in mind when writing your own code - always test on a genuine A1200 as well.
- This effect is not limited to the unexpanded A1200. It will also work on the CD32, A4000 and -in principle- the A3000. The percentage of performance gained may be slightly different on the A4000 and A3000. In general, I expect the A4000 to do better and the A3000 to do a bit worse than the A1200. However, I do not have access to an A3000 or A4000 to test this assumption.
- The performance gain is dependent on many variables. First and foremost it depends on the algorithm used - I provided optimised and generic routines and the optimised routines deliver better performance than the generic ones. That said, the generic ones do offer better performance than just using the Blitter.
- Performance somewhat scales with size of object. Generally, the bigger the object, the better.
- Very thin objects (16 pixels wide or less) are not likely to gain any performance using the routines I provided. It may be possible to write routines that do offer an increase for even these objects, but these are not currently included.
- Using my routines, objects that are not multiples of 32 pixels wide will perform identically to the nearest higher object size that is a multiple of 32 pixels wide. It's possible to write routines that improve this at the very least when these objects are blit aligned to a 32 pixel boundary and with a shift of less than 16 pixels. In fact, such a routine will improve performance of these objects beyond the level currently seen. However, such a routine will not improve performance for these objects if they are not aligned to 32 pixel boundaries or are aligned to such a boundary but need a shift of more that 16 pixels.
- In general, the 68020 in the A1200 is slowed down significantly if it is required to read or write a longword to an address that is not divisible by four.
- Accelerators may prove a small challenge. Some A1200 accelerators have slow access speeds to chip memory. This can be an issue as this effect demands a high access speed to work well. I've thought of a workaround. It's possible to copy the bob and mask data to fast memory as well as keeping it in chip memory. Doing so will most likely solve any such problems as this will reduce the amount of data the CPU needs to read by as much as 50%, letting it be read from the much faster memory of the accelerator instead.
- In general, this algorithm is designed and optimised for unexpanded Amiga's. When using an accelerated Amiga, there are better options available to improve graphics performance (even though it's possible these would still benefit from the Blitter also running - which might be an interesting thing to test for people programming aiming at such environments)
- The generic routines provided in the source code are designed as examples. They are not designed to be the fastest possible, though using them will still improve blitting speed (especially for bigger objects). Keep this in mind when implementing (part of) this code.
- I have considered several ideas that might increase performance further but have decided to not implement them in this example. The idea here is to offer a starting point that is still easy to understand. Which is also why there are so many comments in the code.
- Considering this is my first attempt at writing code like this, I'm fairly certain that possibility for optimisation still exists.
As can be seen by looking at the results, the use of the 68020 in the A1200 to support the Blitter offers a modest increase in performance. It also requires a bit of thought about what objects to use this method for and might require some extra routines to be useful for certain object widths. All that said, I'm rather pleased with the result.
Not only did I learn a lot about the A1200 and the 68020 while making this, I've also managed to do something I genuinely did not expect: make a cookie-cut Blitter+CPU algorithm on the 68020 that is actually useful. And I managed to find a way to make this relatively easy to use: all that really changes in programs using this method is having a different set of blitting routines and calling them instead of the standard ones that use just the Blitter.
Even the performance isn't all that bad, getting somewhere around 13% extra blitting speed is not exactly useless, it might even be enough to help make some things possible that previously were not.
I could write for another 10 pages on ideas that I still have, or the challenges of making this run well on a genuine A1200 (Amiga emulators don't quite emulate the 68020 perfectly, causing different levels of performance on the emulator vs a real Amiga). Or about how many things went wrong (my first attempt didn't align to 32 bit boundaries, causing radical drops in performance when bobs were misaligned). However, I think I'll end it here.
I see the routines I've created for this program as a starting point for myself (and hopefully others) to consider these kind of methods. I also hope it will lead to programmers looking at other out-of-the box ideas when coding for the A1200. As a result of doing this project, I've become more convinced that the unexpanded A1200 has more to offer than we've generally seen, particularly for games. The A1200 got some very good games in 2019, let's hope that ideas like these will help to get even more and even better games for it :)
Not only did I learn a lot about the A1200 and the 68020 while making this, I've also managed to do something I genuinely did not expect: make a cookie-cut Blitter+CPU algorithm on the 68020 that is actually useful. And I managed to find a way to make this relatively easy to use: all that really changes in programs using this method is having a different set of blitting routines and calling them instead of the standard ones that use just the Blitter.
Even the performance isn't all that bad, getting somewhere around 13% extra blitting speed is not exactly useless, it might even be enough to help make some things possible that previously were not.
I could write for another 10 pages on ideas that I still have, or the challenges of making this run well on a genuine A1200 (Amiga emulators don't quite emulate the 68020 perfectly, causing different levels of performance on the emulator vs a real Amiga). Or about how many things went wrong (my first attempt didn't align to 32 bit boundaries, causing radical drops in performance when bobs were misaligned). However, I think I'll end it here.
I see the routines I've created for this program as a starting point for myself (and hopefully others) to consider these kind of methods. I also hope it will lead to programmers looking at other out-of-the box ideas when coding for the A1200. As a result of doing this project, I've become more convinced that the unexpanded A1200 has more to offer than we've generally seen, particularly for games. The A1200 got some very good games in 2019, let's hope that ideas like these will help to get even more and even better games for it :)
Above: the CPU Assisted Blitting program explained and showed in action.
In conclusion, this effect offers a nice boost to blitting performance on the unexpanded A1200 (and other machines using 32 bit Chip memory). It does this for a relatively small cost in extra code complexity. My personal opinion is therefore that it's a worthwhile tool to add to your arsenal when writing demanding games or demos that target a basic A1200. What personally surprised me is that even cookie-cut blits can be sped up by a reasonable amount. I didn't really expect that result when starting this.
I hope this is a useful example and maybe it will inspire coders to implement similar blitting code in games (or perhaps even demos).
All code, apart from the startup code (by Photon of Scoopex), the joystick code (found on eab.abime.net) and the random number generator (by Meynaf, as found on eab.abime.net) was written by me and is (C) 2020 Jeroen Knoester.
That said, please do use any part of my code or this idea you find useful. A credit/mention would be nice but is not required in any way. The program, source code and a bootable .ADF can be found in the downloads section.
If you have any questions, be sure to contact me through the contact form!
I hope this is a useful example and maybe it will inspire coders to implement similar blitting code in games (or perhaps even demos).
All code, apart from the startup code (by Photon of Scoopex), the joystick code (found on eab.abime.net) and the random number generator (by Meynaf, as found on eab.abime.net) was written by me and is (C) 2020 Jeroen Knoester.
That said, please do use any part of my code or this idea you find useful. A credit/mention would be nice but is not required in any way. The program, source code and a bootable .ADF can be found in the downloads section.
If you have any questions, be sure to contact me through the contact form!